未来的日活预测算法
我们经常会面临这么一些问题,比如:
1. 如果维持当前的产品功能不变、投放不变,那么产品的日活会稳定在什么水平?
2. 如果希望产品最终达到百万日活,那么应该维持多少的每日新增?
首先,我们需要认识到如果一个产品有稳定每日1w的新增设备,并不意味着这个产品的日活会无限涨上去,因为现有用户总是在不断的流失,如果产品功能不变,也意味着留存率不变,当日活体量越大,那每天流失的用户就越大,总归有一天正好每天流失1w用户,那么新增与流失相抵消,日活也就稳定下来,不再上涨。
然后,产品的前期投入总是效果明显,而日活达到一定量后,投放同样多的钱,日活上涨的幅度会越来越小,直到趋近于零。所以并不是减小投放后,日活百万的时间点往后移的问题,而可能是永远也达不到日活百万的问题。
那怎么做日活的未来预测呢?
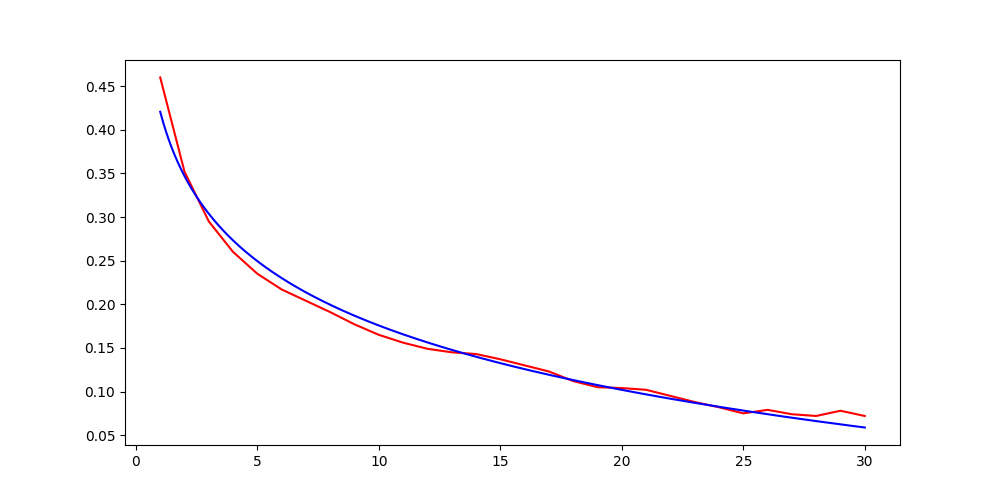
首先需要一个留存表,比如我们知道D0~D30的新增设备留存率,那么我们就可以在图上进行标注,然后进行函数拟合,比如我们用y = A * ln(x) + B进行拟合,我们需要计算出这里的A和B,可以用python函数leastsq()做最小二乘法求拟合系数:
import numpy as np
from scipy.optimize import leastsq
import pylab as pl #matplotlib
import math
#定义函数
#y = A * ln(x) + B
def func(x, p):
A, B = p
return A * np.log(x) + B
#定义残差函数
def residuals(p, y, x):
return y - func(x, p)
x0 = range(1, 31)
x2 = np.array(x0)
y0 = [
46.0 / 100,
35.2 / 100,
29.5 / 100,
26.0 / 100,
23.5 / 100,
21.7 / 100,
20.4 / 100,
19.1 / 100,
17.7 / 100,
16.5 / 100,
15.6 / 100,
14.9 / 100,
14.5 / 100,
14.3 / 100,
13.7 / 100,
13.0 / 100,
12.3 / 100,
11.2 / 100,
10.5 / 100,
10.4 / 100,
10.2 / 100,
9.5 / 100,
8.8 / 100,
8.2 / 100,
7.5 / 100,
7.9 / 100,
7.4 / 100,
7.2 / 100,
7.8 / 100,
7.2 / 100,
]
y2 = np.array(y0)
p0 = [0.5,0.5] #取值起始点
qs = leastsq(residuals, p0, args=(y2,x2))
A, B = qs[0]
print(A, B)
拟合出来的结果为y = -0.10640986 * ln(x) + 0.4207124:
因为是一个对数函数,所以跟x轴会有交点,也就是在某个时间点之后,我们简单认为用户再也不会回来了,于是我们可以计算出设备的存活天数:
max_days = int(math.e ** (-B / A))
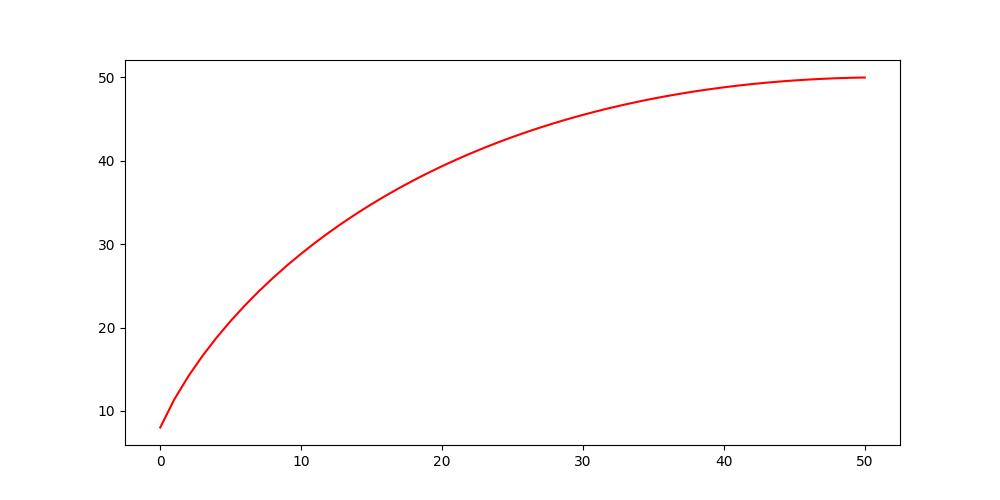
有了这个留存曲线之后,如果我们知道每日新增稳定在多少,我们就可以知道从第一天开始,日活每天会怎么变化,直到max_days变成稳定:
计算代码为:
daus = []
for i in range(1, max_days):
daus.append(x * (1 + sum(func(i, qs[0]) for i in range(1, i))))
接着,我们查看最近一天的日活,就知道处于该日活曲线的什么位置,就知道还有多少天可以上涨,以及未来会平稳在多少数量上。
发表于 2022年05月04日 15:48 评论:0 阅读:3758