关于方差Variance

高中学习的方差是这么算的：

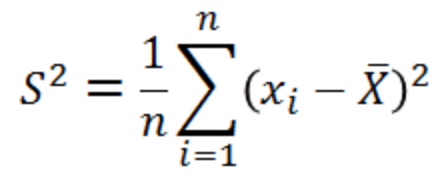
S为标准差，S^2就是方差，或者表示成Var(X)。

而实际中我们不能穷尽样本，而是采样的方式来计算均值，这样就导致采样不一样，均值也不一样，所以这里的均值也成了一个随机变量。

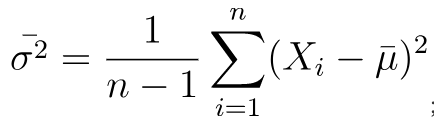
结果除以n，就变成了除以n-1。（请忽略这里的符号不统一，毕竟是到处截的图）

关于方差的除以n-1，主要是为了无偏估计。无偏估计定义为：在多次重复下，它们的平均数接近所估计的参数真值。

至于如何理解，有两种方式，一种是所谓的自由度，另一种是公式推导。两种方式都有让我不太好接受的地方。

自由度是说有多少变量是可以自由变化的，而N个样本确定，均值确定之后，其实只有n-1个变量可以变化，所以自由度为n-1。例如假设样本有3个值，即x1=2,x2=4,x3=9,则当 x拔 =5确定后，x1、x2、x3只有两个数据可以自由取值，另一个则不能自由取值，比如x1=6,x2=7,那么x3必然取2，而不能取其他值。方差是衡量变量变化强度的，所以就除了自由度n-1了。

公式推导如下，根据如下等式：

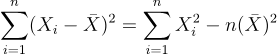
方差的期望就是：

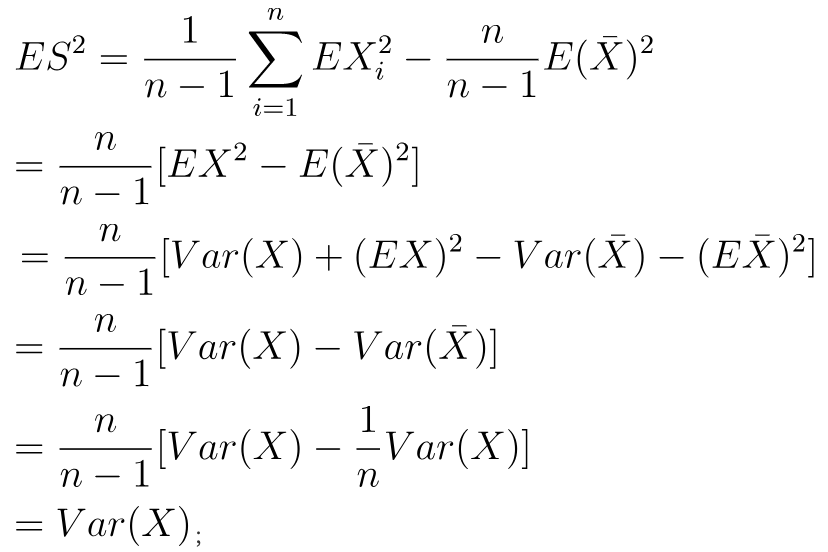
该证明能成功的关键等式为：

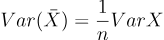
这个等式让人琢磨不透，留着以后慢慢琢磨吧。

总之，在高中课本中讲到的方差是除以n，该n为全部数据的个数。而实际运用中使用的是n-1，该n表示的是抽样样本个数。无偏估计则说明在多次抽样过程中，只要抽样次数足够多，那么方差计算值就跟真实值越接近。