关于协方差Covariance
结合网络上关于协方差矩阵的公式推导和numpy库使用,实现协方差矩阵的计算,确切地说是相关系数矩阵。
协方差
协方差反映的是两个随机变量之间的线性相关程度,将程度值归一化到一个[-1, 1]的范围区间内,就得到相关系数,以便于理解和评估线性相关程度。特别注意:是线性相关。当一个随机变量变大,另一个随机变量也会变大,这就是正相关,相关系数会在[0, 1]之间,反之,如果在[-1, 0]之间,就是负相关。如果两个随机变量满足kx + b这样的严格线性关系,那么k>0时,相关系数为1,k<0时,相关系数为-1。
计算公式:
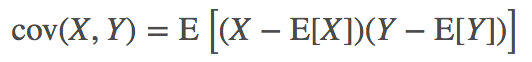
一个随机变量与自身的协方差,就是方差:
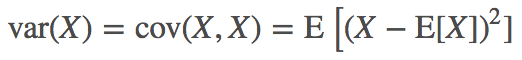
相关系数
协方差归一化后的相关系数,更便于多个随机变量之间的比较,相关系数公式为:
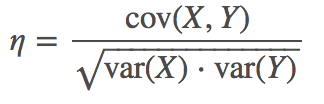
在实际中,通常我们手头会有一些样本,样本有多个属性,每个样本可以看成一个多维随机变量的样本点,我们需要分析两个维度之间的线性关系。协方差及相关系数是度量随机变量间线性关系的参数,由于不知道具体的分布,只能通过样本来进行估计。
设样本对应的多维随机变量为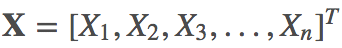 ,样本集合为
,样本集合为 ,与样本方差的计算相似,a和b两个维度样本的协方差公式为:
,与样本方差的计算相似,a和b两个维度样本的协方差公式为:
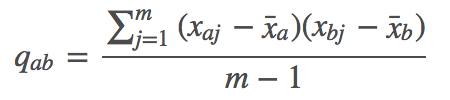
这里分母为m−1是因为随机变量的数学期望未知,以样本均值代替,自由度减一。
协方差矩阵
对多维随机变量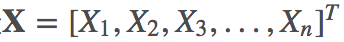 ,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差:
,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差:
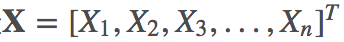 ,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差:
,我们往往需要计算各维度两两之间的协方差,这样各协方差组成了一个n×n的矩阵,称为协方差矩阵。协方差矩阵是个对称矩阵,对角线上的元素是各维度上随机变量的方差: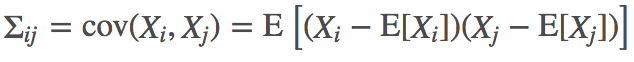
矩阵完整表示为:
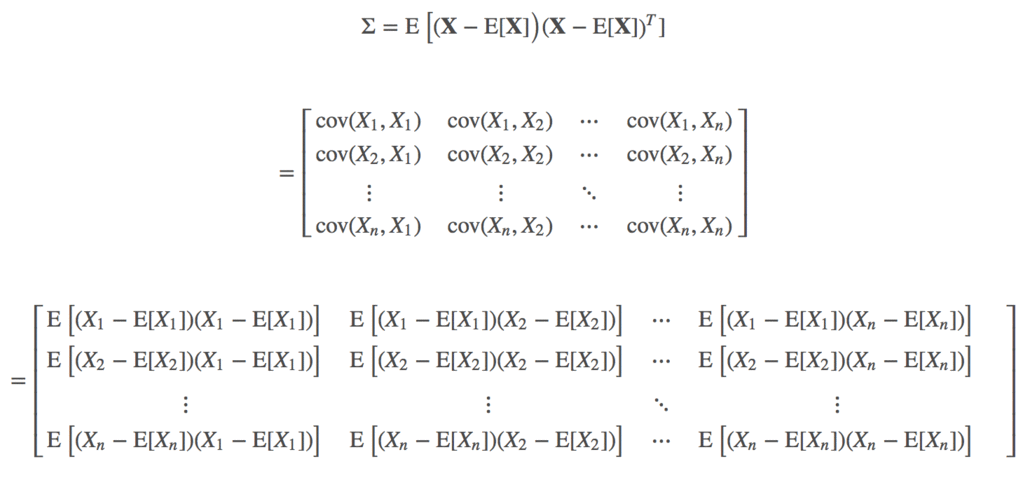
基于样本数据的协方差矩阵公式即为:
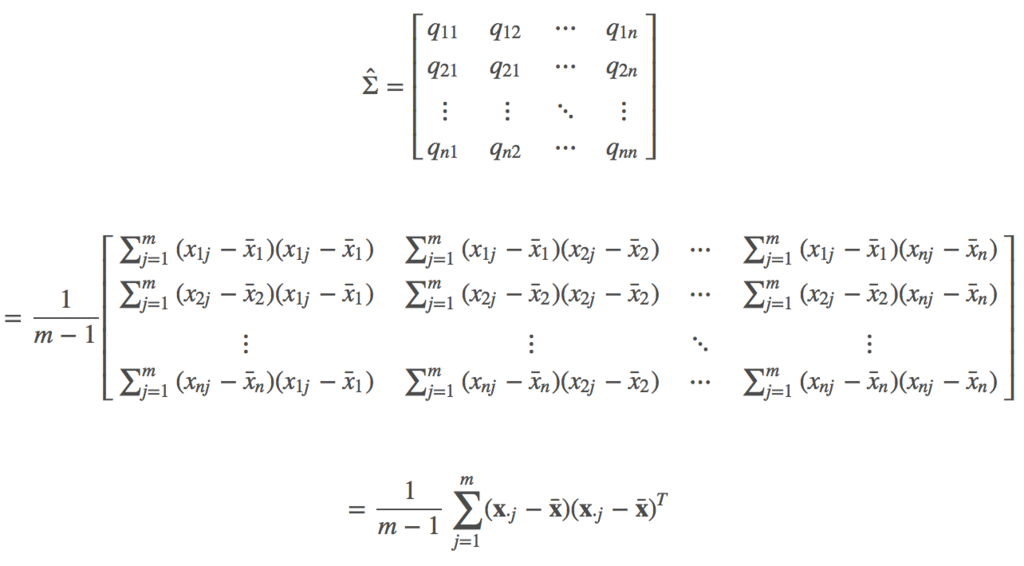
确实可以两两计算协方差,然后再来填充这个矩阵,而直接通过矩阵运算,来得到协方差矩阵,性能更佳。
相关系数矩阵
很多时候我们只关注不同维度间的线性关系,且要求这种线性关系可以互相比较。所以,在计算协方差矩阵之前,通常会对样本进行归一化,包括两部分:

这样公式就
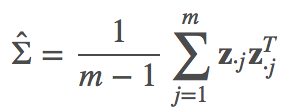
基于numpy的代码实现
python函数实现协方差、相关系数、协方差矩阵等:
import numpy as np
X = np.arange(10, dtype=np.float32)
#Y = 2 * X + 1 * np.random.rand(10)
Y = 2 * np.exp(X) + 1 * np.random.rand(10)
def variance(l):
avg = sum(l)/len(l)
return sum((avg - i)**2 for i in l) / (len(l)-1)
def covariance(a, b):
avg_a = sum(a) / len(a)
avg_b = sum(b) / len(b)
return sum((ai - avg_a) * (bi - avg_b) for ai, bi in zip(a,b)) / (len(a)-1)
def conv_matrix(*arr):
"""计算协方差矩阵,其实是计算相关系数矩阵"""
matrix = np.array(arr, dtype=np.float32)
for i,a in enumerate(matrix):
avg = np.average(a)
var = variance(a)
#matrix[i] = (a - avg) #不归一化就是协方差矩阵,归一化就是相关系数矩阵
matrix[i] = (a - avg) / var ** 0.5
rowNum, colNum = matrix.shape
resM = np.zeros((rowNum, rowNum), dtype=np.float32)
for f in range(colNum):
t = matrix[:,f]
squareMat = np.row_stack([t] * len(t))
resM += squareMat * squareMat.T
resM /= colNum - 1
print(resM)
print(X, Y)
varX = variance(X)
print(varX)
varY = variance(Y)
print(varY)
res = covariance(X, Y) / (varX * varY) ** 0.5
print(res)
conv_matrix(X, Y, X)
输出为:
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [2.28564822e+00 6.12990148e+00 1.51675016e+01 4.11676113e+01
1.09295178e+02 2.96868290e+02 8.06930621e+02 2.19363561e+03
5.96228109e+03 1.62062138e+04]
9.166666666666666
26446060.727093935
0.7168583584644617
[[0.9999999 0.7168583 0.9999999]
[0.7168583 1.0000001 0.7168583]
[0.9999999 0.7168583 0.9999999]]
当然,numpy函数库本身也提供了协方差矩阵的计算函数,使用时不需要自己实现。特别注意:numpy的函数均除以m,而不是m-1,不过无论是无偏估计还是有偏估计,相关系数的计算中都会约去,比较相关性时无影响:
np.var(X) #方差
np.cov([X, Y, X]) #协方差矩阵
np.corrcoef([X, Y, X]) #相关系数矩阵
发表于 2018年08月08日 14:39 评论:0 阅读:9674